Orbital Parameters and Coordinate Frames
Perigee and Apogee
The perigee and apogee are respectively the closest and furthers points of the orbit from the Earth's surface. This apparently simple definition has some complications.
In the strictest meaning of the words, the perigee and apogee are
points
in an elliptical
orbit at which the orbiting object has the smallest and largest radius vectors respectively.
They lie at opposite ends of the semi-major axis of the ellipse.
We often refer to the perigee and apogee
heights;
i.e. the height of the perigee and apogee
points above the planetary surface. Loosely, we drop the word `height' and refer to
these values simply as the perigee and apogee.
But complications arise when you start thinking about the fact that the Earth is not actually
a sphere, but (to a much better approximation) an oblate spheroid - its cross-section is also
an ellipse. Depending on the orientation of the orbit, the two ellipses are misaligned.
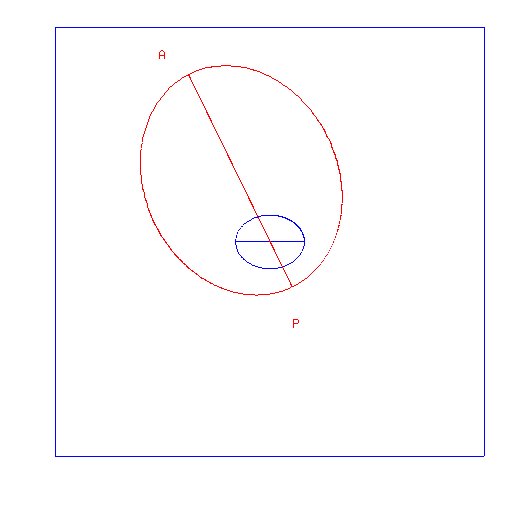
In the figure below, a satellite orbit in red is drawn around an exaggerated Earth in blue.
In this case,
the smallest height of the orbit around the spheroid Earth
is not necessarily the height of the perigee point P. In fact
in the example shown, the point of smallest height is about 40 degrees further around
the orbit.
Worse yet, the flattening of the Earth means that the orbit is not actually an
ellipse. The instantaneous (`osculating') orbital parameters
change with time
as you go round the orbit, so the true perigee and apogee are different from ones
obtained from time-averaged `mean elements'.
It is conventional in space situational awareness contexts to quote perigee and apogee heights
relative to a fictitious perfectly spherical Earth with radius equal to the equatorial radius.
There are a lot of reasons that this makes good sense, but the reader should remember
that the actual height above the Earth may be considerably higher if the perigee is over the
polar regions.
The Friends of Perigee and Apogee
The `gee' in apogee and perigee is from the Greek word for the Earth. For orbits around other bodies, special names are in use. Most of these are falling out of favour and are being replaced by the terms periapsis and apoapsis, referring to the `apsis' (plural, apsides), the generic name for the extreme points in the orbit. There are several terms used for selenocentric orbits. I list terms that I've seen in relatively recent use; there are many others. I'm torn between the poetry of them and the fact that they are totally unnecessary.| Central body | Terms | Plural |
|---|---|---|
| Still in use | ||
| Earth | perigee, apogee | -gees |
| Sun | perihelion, aphelion | -helia |
| Moon | perilune, apolune | -lunes |
| Moon | periselene, aposelene | -selenes? |
| Mars | periares, apoares | -ares |
| Jupiter | perijove, apojove | -joves |
| Star | periastron, apoastron | -astrons |
| Galaxy | perigalacticon, apogalacticon | -icones? (not used) |
| Probably obsolescent | ||
| Moon | pericynthion, apocynthion | -cynthia |
| Venus | pericytherion, apocytherion | |
| Saturn | perikrone, apokrone | |
| Black hole | peribothron, apobothron | -bothroi |
Coordinate Frames and Units
The orbital inclination (and the node and argument of perigee, which are not given in this release of GCAT) depends on the equator and pole of your coordinate frame.
In GCAT, angles are always expressed in degrees and distances are usually in km (but
see below for heliocentric orbits).
- Earth orbits are given with respect to the equator of date (strictly, TEME equator). Note that astronomical positions are often given with respect to the (inertially fixed) ICRF frame. The Earth wobbles due to precession, so the equator of date changes with time relative to the ICRF. Distances are always given in km.
- Heliocentric orbits are given with respect to the J2000 ecliptic. Distances (aphelion and perihelion) are given in astronomical units (AU). 1 AU = 149597870.700 km.
- Orbits around other central bodies (Moon, Mars, etc.) are given with respect to the IAU equator of that body. Where no IAU equator is yet defined in JPL Horizons, the ecliptic is used instead. Distances are given in km.