Solar System Model
GCAT Release 1.8.0 (2025 Nov 10) | Data Update 2026 Jan 17Solar System Description Files
At any given time, an artificial space object is considered to be orbiting a particular astronomical body.
In the General Catalog the body is identified by a string identifier (e.g. "Earth"). The bodies and
their properties are described in two files, the Worlds file and the Spin file.
Preamble: The Hill Sphere
In general, a space object travels under the gravitational influence of all the massive
worlds in the system. However, in most cases the effects of all but one body can
be neglected or treated as small perturbations. We say that the object is `in orbit
about' that one body. (The orbit is not necessarily bound; it may be a hyperbola rather than
an ellipse). I introduce the concept of the Hill sphere of body A with
respect to body B.
Let the mass of body A be M, the (smaller) mass of body B be m,
and the distance between A and B be R. Then B's gravity dominates (in this approximation)
when the distance from the object to B is less than
r(Hill) = R (m/3M)(1/3)
For example, the radius of the Sun-Earth Hill sphere is about 1.5 million km centered
on the Earth. The radius of the Earth-Moon Hill sphere is about 66,000 km centered
on the Moon, and therefore is entirely within the Sun-Earth sphere.
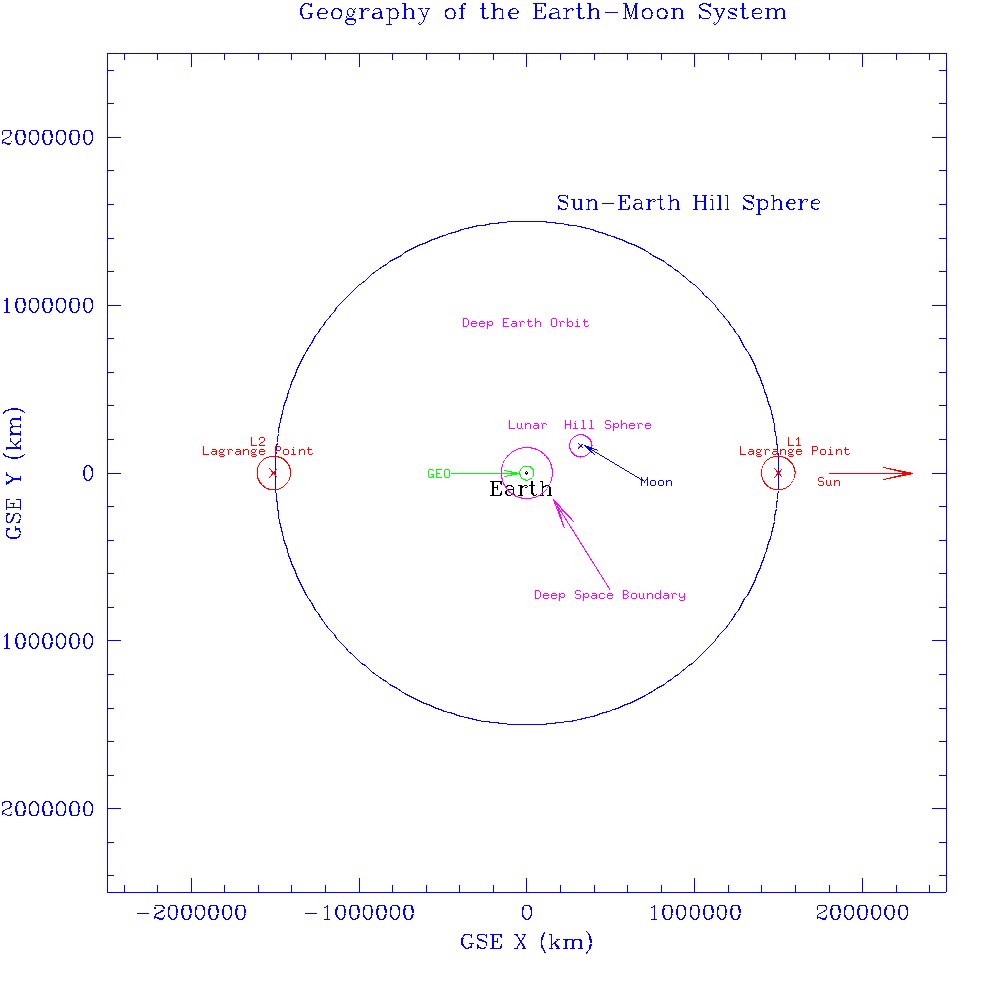
Here is a map of the Earth-Moon system (with the Moon's position shown on the arbitrary
date of 1968 Dec 21), showing the sizes of the two Hill spheres.
The map is in geocentric solar ecliptic coordinates in which the Earth-Sun line is fixed and is the X-axis.
The locations
for the SEL1 (Sun-Earth Lagrange 1) and SEL2 (Sun-Earth Lagrange 2) points (see below) are also shown. The magenta
circle around the Earth indicates the EL1:4 `deep space boundary' beyond which I record space objects
in the Deep Space Catalog instead of the main Earth satellite catalog.
Worlds in the Solar System
The General Catalog includes data on spacecraft in the vicinity of
bodies throughout the Solar System (and, like the Voyagers, on their
way to the great beyond).
We consider four kinds of body:
- Stars, of which the only one currently relevant to space travel is the Sun.
- Worlds. A world is a body which is sufficiently massive that it is spheroidal due to its own gravity but not massive enough to be a star. This includes gas and ice giants like Jupiter and Neptune, and terrestrial rocky and icy worlds like Earth and Titan. The majority of worlds are icy bodies beyond Neptune whose sizes are in fact poorly known at the moment.
- Small bodies, solid objects smaller than worlds - asteroids, comets, small moons, and small Trans-Neptunian objects. While the true geophysical boundary between worlds and small bodies depends on composition, for definiteness I treat all substellar bodies with mean radius more than 200 km as worlds. In the list of small bodies used in the catalog, I include a number of the larger ones and all bodies that have been visited by spacecraft.
- Dynamical reference points, of which we consider two types: subsystem barycenters and Lagrange points.
Objects maintaining position near Lagrange points are recorded in the General Catalog as `orbiting'
those points; in all other cases, objects are considered to orbit the body whose Hill sphere they
are within. (In the case of nested Hill spheres, we take the innermost sphere the object is within).
Dynamical Reference Points
First, let's discuss barycenters.
- The SSB: of greatest importance is the Solar System Barycenter (SSB), the center of gravity of the Solar System. We often choose coordinates in which the planets orbit the Sun (HC, heliocentric coordinates), and that's what I do for the most part in the General Catalog. But you can instead use a barycentric coordinate (BC) system in which the Sun and the planets jointly orbit the SSB, and this is actually `better' or `more correct' in several senses - for example, BC is closer to an inertial frame, and orbital elements of loosely bound objects like high-eccentricity comets are less time-variable in BC. I went back and forth a few times on this but ultimately decided to stick with object-centered systems (HC and geocentric), partly because it's conventional to refer Earth satellites to the Earth's center and not the Earth-Moon barycenter.
- The EMB: the Earth-Moon Barycenter. It is useful to think of the EMB as orbiting the Sun and the Earth and Moon as each orbiting the EMB. (The EMB's orbit around the Sun is more closely an ellipse, while the Earth's has wobbles in it due to the Moon).
- Other subsystem barycenters, notably the Jovian and Saturnian systems (whose barycenters, however, are deep within their central planets). These are not explicitly in the attached world list, but are automatically added to the list in software as needed.
Now let's talk about Lagrange points, which are closely related to the Hill sphere discussed in the
previous section. When body B orbits body A, an object orbiting both will be subject to the effects of the gravity
of A and B and to the acceleration due to the angular momentum it has with respect to both. Lagrange showed that the
net effective forces balance at five points which are the solution of a quintic equation, the Lagrange quintic.
We refer to these points as the L1 to L5 points of the A-B system. The Lagrange points for the
specific and special A-B cases of Sun-Earth and Earth-Moon are referred to as SEL1 to SEL5 and EML1 to EML5.
- The L1 point lies at the interior intersection between the A-B line and the A-B Hill Sphere. SEL1 is 1.496 million km from the Earth in the direction towards the Sun (i.e. towards noon). SEL1 is useful for probes studying solar wind particles before they reach the Earth.
- The L2 point lies at the exterior intersection between the A-B line and the A-B Hill Sphere. SEL2 is 1.496 million km
from the Earth in the direction away from the Sun (i.e. towards midnight). SEL2 is very useful
for astronomical observatories. EML2 is being used by the Queqiao communications spacecraft as a farside communications
relay point.
The L1 and L2 points are peaks in the effective potential; gravitational forces on objects there are low but nonzero and slowly cause the object to drift away. However, these forces can be counteracted by occasional small thruster firings. In practice spacecraft are placed in large `orbits' around L1 or L2, with radii often in the hundreds of thousands of km for SEL1/2 and maintenance thruster burns every few months. I put the quotes around the word `orbit' since there is of course no central gravitating mass at the Lagrange point, and the paths are not remotely Keplerian. Lagrange trajectories can be either `halo orbits' or `Lissajous orbits', and I hope to finally get around to learning the relevant orbital dynamics some day soon. - The L3 point lies on the extension of the A-B line through A, roughly at the same distance from A as B is. SEL3 is therefore about 149.6 million km from the Sun and 180 degrees around the Earth's orbit from Earth - it is, roughly, the Anti-Earth. At least so far, the L3 point has not had any particular importance in astronomy or astronautics.
- The L4 and L5 points make an equilateral triangle with A and B, in the plane of the A-B mutual orbit. Unlike L1 to L3, they are gravitationally stable. The first practical example of Lagrange points was the discovery of asteroids at Sun-Jupiter L4 and L5. These asteroids were given names of characters from the Trojan War and became known as Trojan asteroids; the L4 and L5 points are thus also known as `Trojan points' of any A-B system. Some probes have explored the interplanetary environment near the Earth-Moon L4 and L5 points.